中高一貫校は、中学と高校で分断されることなく、6年間を一つの流れとして捉えて、教育を進めていきます。
そのため、効果的なカリキュラムの組み方ができるのですが、いっぽうで落とし穴になっている部分もあると感じています。
高速カリキュラム
学びのレベルにばらつきがあると、どうしても遅れがちな子をケアしながら進めるため、カリキュラムをどんどん進めるということができません。
しかし中高一貫校の場合には、中学受験を乗り越えてきた子どもたちが集まっているため、一定以上のレベルの学びの力を持っている集団だと言えます。
その集団の標準的なレベルに合わせた授業を設計するにしても、標準的なレベルというそのものが一般的なレベルよりも高いところにあります。
そのため、高いレベルでのカリキュラムを組むことができるのです。
その一つが、高速カリキュラムです。
まず学習指導要領で、中学・高校のカリキュラムを見てみます。
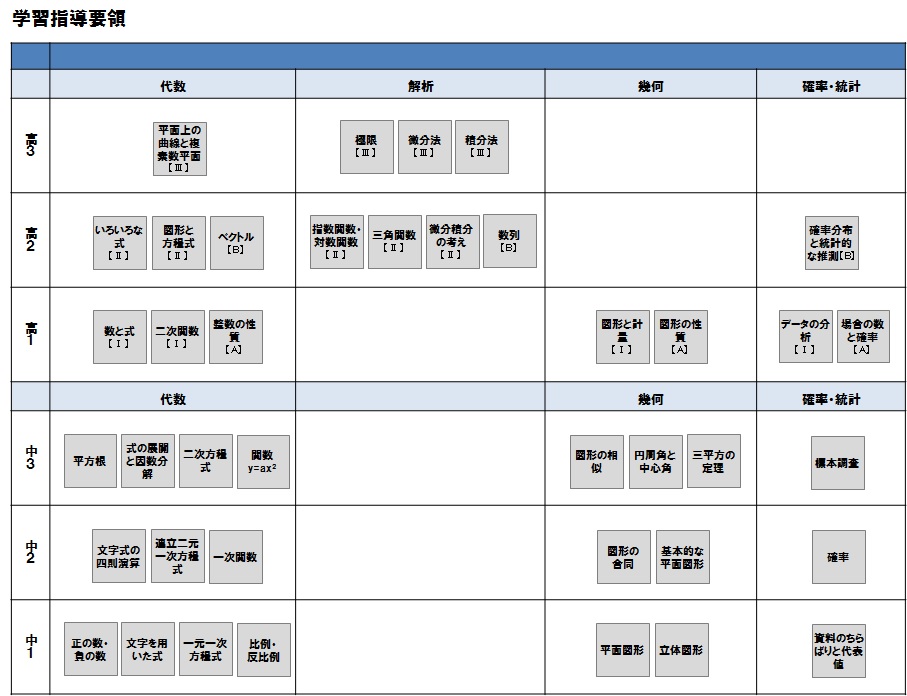
あたり前ですが中3で中学課程を修了し、高1で数学ⅠA、高2で数学ⅡB、そして理系は高3で数Ⅲと進んでいきます。
いっぽうで中高一貫校で使用される体系数学のカリキュラムを見てみます。
(高校課程からは、青チャートやフォーカスゴールドを使うと思いますが)

中1~中2: 中学課程を修了
中3: 数ⅠAを終了
高1: 数ⅡBを終了
高2: 理系は数Ⅲ、文系は数ⅠA/数ⅡBの演習
となり、高1の段階で文系であれば高校数学の範囲を終えてしまいます。
数Ⅲのある理系でも、高2で高校数学の範囲を終えます。
たとえば連立方程式や一次関数は、学習指導要領であれば中2の範囲です。しかし体系数学を使っていると、それは中1で学習することになるのです。
学習指導要領と比較して見ると、その差は歴然とします。
このスピードでも、基礎の定着重視に絞って進めれば、それはそれで良いと思うんですよね。
しかし、そうそうはうまくいかないのが現実で・・・
そんな問題を解かせるの?
中学受験を乗り越えてきた子は、算数/数学が得意な子が多い。
特に男子はそうだと思います。
そういう子は、基礎的な問題演習では飽きてしまいます。応用問題を与えて、どんどん解かせていくことで、さらに数学の力が伸びていくと思います。
そのため普段の宿題でも、平気で応用問題まで含めて範囲にしますし、数学の定期テストでも前半こそ基本問題ではあるものの、後半は応用問題を出してきたりします。
数学のできる子に寄り添いつつ、定期テストでもしっかりと差が出るように考えられているのだと思います。
しかしですね、そういう子は、東大入試で言えば、理系の数学で6問ほぼ完答とか、5問完答1問半答とか、文系数学でほぼ4問完答とかといったレベルに到達できる可能性のある子なんです。それって、理Ⅲに合格したり、理Ⅰをトップクラスで合格したりする子です。
駿台が東大受験者の得点開示集計を分析していますが、理Ⅰや理Ⅱの合格者の数学での平均点は120点満点中60点ぐらい、文系の合格者の平均点は80点満点中35~50点ぐらいなんですよね。(年度によって難易度に差があるので、ばらつきますが)
理Ⅲは別として、他の科類であれば、半分ぐらい得点できれば合格者平均なんです。
文系であれば全4問のうち、2問完答2問半答できれば50点強になるので、他の教科で失敗しなければ合格圏内に十分到達します。
そして全4問のうち、だいたい2問ぐらいは標準レベルの問題と言われ、残りの2問の難問も小問誘導で最初の小問だけであれば、そこまで難しくないということも多くあります。
なにが言いたいかというと、標準的な問題をしっかりと解ききる力があれば、十分に合格に近づけるのです。
数学で本当に大切なのは、基礎に流れている考え方をしっかりと身につけられるかということです。
もちろん計算力は必要です。ですが、本当に必要なのは、なぜこのような式を立てるのか、なぜ置き換えをするのか、なぜ場合分けをするのか、なぜ範囲を区切って考えるのか、などといったことを、理解した上で解けるようにするということです。
なにが落とし穴か
高速カリキュラムと問題の難易度の高さから、本人は完全にオーバーフローしていました。
とりあえず定期テストで及第点は取っていたものの、基礎的な「理解」がまったく追いついていなかったのです。
中2の時に、数学の問題を教えてもらうふりをして、いろいろと質問をしてみて、そのことがはっきりと分かりました。
高校数学で同じことをやると取り返しがつかなくなります。
そこで中2の冬に、本人と話をしました。
反抗期真っ盛りの中2ではありますが、本人も薄々は「やばい」と感じていたようです。お互いの納得のもと、中3から数学は塾に週1日通うこととしました。
中高一貫生向けのコースなので、中3で高校の数学ⅠAを習うことになります。学校の進度がとても速いので、実は塾で復習ができるようなスピードとなります。
本人には、「学校の定期テストの後半に出てくる難しい問題を解けるようになる必要はない。学校で習ったはずなのに、塾で似たような問題が出てきても解けないということがないようにだけしよう。」ということで、その後も塾のお世話になりながら、数学で落ちこぼれないようにしていました。



